差分约束系统
Intervals
| Time Limit: 2000MS | Memory Limit: 65536K | |
|---|---|---|
| Total Submissions: 28426 | Accepted: 10975 |
Description
You are given n closed, integer intervals [ai, bi] and n integers c1, ..., cn.
Write a program that: reads the number of intervals, their end points and integers c1, ..., cn from the standard input, computes the minimal size of a set Z of integers which has at least ci common elements with interval [ai, bi], for each i=1,2,...,n, writes the answer to the standard output.Input
The first line of the input contains an integer n (1 <= n <= 50000) -- the number of intervals. The following n lines describe the intervals. The (i+1)-th line of the input contains three integers ai, bi and ci separated by single spaces and such that 0 <= ai <= bi <= 50000 and 1 <= ci <= bi - ai+1.
Output
The output contains exactly one integer equal to the minimal size of set Z sharing at least ci elements with interval [ai, bi], for each i=1,2,...,n.
Sample Input
53 7 38 10 36 8 11 3 110 11 1
Sample Output
6
差分约束
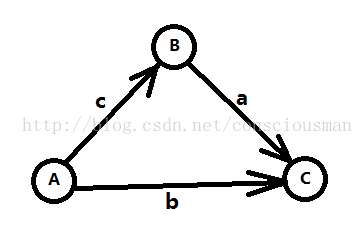
引用一个图片,写过spfa应该能秒懂差分约束,SPFA的松弛操作,dist[AC] <= dist[ A->C的其他路 ]即b<=a+c
另一个问题有一系列不等式
B - A <= c
C - B <= a
C - A <= B
把减法移到另一边,就和我们的松弛操作很像了
详情
题意:给定n个区间,[ai,bi]这个区间至少选选出ci个整数,求一个最小集合z,满足每个区间的要求,输出集合z的大小。
分析:令d[i]表示0到i这个区间内至少要选出d[i]个数,那么对于每个[ai,bi],有d[b] - d[ai-1] >= ci,同时隐含的一个条件是0 <= d[i] - d[i-1] <= 1,但是因此d[-1]不能表示,令d[i+1]示0到i这个区间内至少要选出d[i+1]个数,然后d[0] = 0,直接求取最长路就行了。
#include#include #include #include #include using namespace std;const int maxn = 5e4 + 7;const int maxm = maxn << 2;const int inf = ~0U>>1;int n, a, b, c, first[maxn], sign;struct Node { int to, w, next;} edge[maxm];void init(){ ///注意这里的maxn for(int i = 0; i < maxn; i ++ ) { first[i] = -1; } sign = 0;}void add_edge(int u, int v, int w){ edge[sign].to = v; edge[sign].w = w; edge[sign].next = first[u]; first[u] = sign ++;}int dist[maxn], inq[maxn], L, R;void SPFA(){ for(int i = L; i <= R; i ++ ) { dist[i] = -inf, inq[i] = 0; } queue Q; Q.push(L); inq[L] = 1, dist[L] = 0; while(!Q.empty()) { int now = Q.front(); Q.pop(); inq[now] = 0; for(int i = first[now]; ~i; i = edge[i].next) { int to = edge[i].to, w = edge[i].w; if(dist[to] < dist[now] + w) { dist[to] = dist[now] + w; if(!inq[to]) { Q.push(to); inq[to] = 1; } } } }}int main(){ while(~scanf("%d", &n)) { init(); L = inf, R = -inf; /** 约束不等式 d[ bi ] - d[ ai - 1] >= ci; d[i] - d[i - 1] >= 0; d[i] - d[i - 1] >= -1; */ for(int i = 1; i <= n; i ++ ) { scanf("%d %d %d", &a, &b, &c); a ++, b ++; add_edge(a - 1, b, c); L = min(L, a - 1); R = max(R, b); } for(int i = L; i < R; i ++ ) { add_edge(i, i + 1, 0); add_edge(i + 1, i, -1); } SPFA(); printf("%d\n", dist[R]); } return 0;}